大数运算
1, 大数存储
数字较大,超过了基本类型的表示范围,因此单个变量无法存储整个数据。我们可以使用数组保存每位数字。比如 123456789123456789 可以这样存储:

以下以十进制为例(没有处理输入为负数的情况,没有处理小数情况,没有设计一个良好的数据结构):
2, 加法
(1)从低位算起,将对应的位相加,再加上前一位的进位,得到结果sum
(2)将sum对10取余,则获得本位对应的数字
(3)将sum除10取整,则获得进位
(4)依次将所有位计算完毕
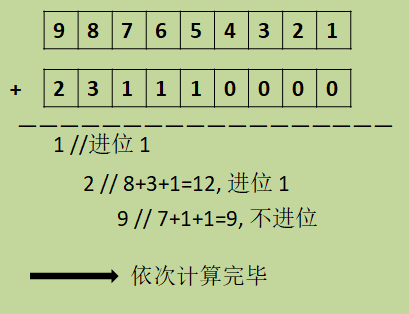
代码如下:
/**
* 计算 a 和 b 的和
* @param [in] a 加数1
* @param [in] aLen 数组a的长度
* @param [in] b 加数2
* @param [in] bLen 数组b的长度
* @param [out] result 计算结果
*
* @return 和的长度
*/
int add(int *a, int aLen, int *b, int bLen, int *result)
{
//以较长的位数作为循环控制条件
int maxLen = aLen > bLen ? aLen : bLen;
int carry = 0;
//从低位到高位依次计算
for (int i = 0; i < maxLen; i++)
{
int tmp = a[i] + b[i] + carry;
result[i] = tmp % 10;
carry = tmp / 10;
}
//处理最后的进位
if (carry > 0)
{
result[maxLen] = carry;
maxLen++;
}
return maxLen;
}
3, 减法
减法略微复杂,但依然采用列竖式的方法,需要处理如下情况:
(1)向高位借位:被减数的某位数字小于减数的,此时需要向高位借1;如果高位是0,我们可以暂时不用继续往更高的位借1,只需要保持此位为负数;比如:100 - 9,个位不够减,往十位借1,十位已经是0,此时把十位记作-1,留到之后处理;
(2)被减数小于减数: 此时需要设置负数标志;

代码如下:
/**
* 比较 a 和 b 的大小
* @param [in] a 数字1
* @param [in] aLen 数组a的长度
* @param [in] b 数字2
* @param [in] bLen 数组b的长度
*
* @return a和b比较结果
* @retval 1 a > b
* @retval -1 a < b
* @retval 0 a == b
*/
int compareNum(int *a, int aLen, int *b, int bLen)
{
if (aLen == bLen)
{
for (int i = aLen - 1; i >= 0; i--)
{
if (a[i] == b[i])
{
continue;
}
return a[i] > b[i] ? 1 : -1;
}
return 0;
}
else
{
return aLen > bLen ? 1 : -1;
}
}
/**
* 计算 a - b
* @param [in] a 被减数
* @param [in] aLen 数组a的长度
* @param [in] b 减数
* @param [in] bLen 数组b的长度
* @param [out] result 计算结果
* @param [out] negative 计算结果的符号
*
* @return 计算结果的位数(result长度)
*/
int sub(int *a, int aLen, int *b, int bLen, int *result, int *negative)
{
int aCopy[MAX_LEN] = {0};
for (int i = 0; i < aLen; i++)
aCopy[i] = a[i];
int bCopy[MAX_LEN] = {0};
for (int i = 0; i < bLen; i++)
bCopy[i] = b[i];
int *value1 = aCopy;
int *value2 = bCopy;
int maxLen = aLen;
//比较大小,将大的作为被减数,同时记录符号位
int comResult = compareNum(aCopy, aLen, bCopy, bLen);
if (comResult < 0)
{
value1 = bCopy;
value2 = aCopy;
*negative = -1;
}
else if(comResult == 0)
{
result[0] = 0;
return 1;
}
//从左到右依次计算
for (int i = 0; i < maxLen; i++)
{
//向高位借位
if (value1[i] < value2[i])
{
value1[i] += 10;
value1[i+1]--;
}
result[i] = value1[i] - value2[i];
}
//去除高位的0,获取结果真实长度(比如912 - 12,数组高位会保存零)
for (int i = maxLen - 1; i >= 0; i--)
{
if (result[i] > 0)
return i + 1;
}
return 0;
}
4, 乘法
参考从列竖式计算乘法的思路:
- 从低位向高位,依次计算
- 将乘数的每一位逐次和被乘数的每一位相乘
(1) 乘数的第一位与被乘数的每一位相乘(从低位到高位),并记录每一位的结果
(2) 乘数的第二位与被乘数的每一位相乘(从低位到高位),并记录每一位的结果,并左移一位
(3) 依次类推,计算完所有的结果
(4) 将所有结果对应位相加,并计算进位,得到最终结果
列竖式计算时,我们每次都把进位计算出来,其实我们可以先不计算进位,比如十位上计算结果是36,先保持不动,等到所有乘法计算完毕,统一处理
以计算153 * 34 为例:
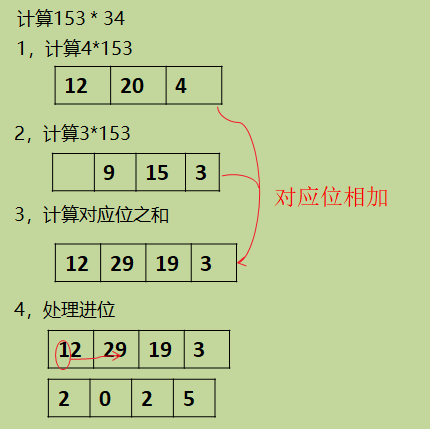
以上我们可以看出,用数字表示两数相乘时: result[i+j] = a[i] * b[j]
如果我们每次都保存每一小步的乘积结果,会浪费很多空间,可以只用一个result数组保存,之后的结果,把对应的位直接累加
/**
* 计算 a * b
* @param [in] a 被乘数
* @param [in] aLen 数组a的长度
* @param [in] b 乘数
* @param [in] bLen 数组b的长度
* @param [out] result 计算结果
*
* @return 计算结果的位数(result长度)
*/
int mul(int *a, int aLen, int *b, int bLen, int *result)
{
// 逐次计算乘积
for (int i = 0; i < aLen; i++)
{
for (int j = 0; j < bLen; j++)
{
result[i + j] += a[i] * b[j];
}
}
// 处理进位
for (int i = 0; i < aLen + bLen - 1; i++)
{
result[i + 1] += result[i] / 10;
result[i] = result[i] % 10;
}
// 处理总长度,两数相乘,最长位数是两个数位数之和
if (result[aLen + bLen -1] > 0)
{
return aLen + bLen;
}
else
{
return aLen + bLen - 1;
}
}
上面的计算方法复杂度是$N^2$, 乘法可以使用分治思想 – karatsuba乘法
Karatsuba算法是一种快速相乘算法,它由Anatolii Alexeevitch Karatsuba于1960年提出并于1962年发表。它将两个n位数字相乘所需的一位数乘法次数减少到了至多 $3n^{\log _{2}3} \approx 3n^{1.585}$(如果n是2的乘方,则正好为 $n^{\log _{2}3}$)。因此它比要 $n^{2}$次个位数乘法的经典算法要快。例如,对于两个1024位的数相乘( n=1024=$2^{10}$ ),Karatsuba算法需要 $3^{10}=59049$ 次个位数乘法,而经典算法需要 $(2^{10})^{2}=1048576$ 次。
基本的原理和做法是将位数很多的两个大数 x和 y分成位数较少的数,每个数都是原来 x和 y位数的一半。这样处理之后,简化为做三次乘法,并附带少量的加法操作和移位操作。

代码如下:
/**
* 对输入数据进行左移操作(类似于pow函数,非二进制)
* @param [in/out] a 输入数据
* @param [in] aLen 数组a的长度
* @param [in] shiftLen 左移位数
*
* @return 计算结果的位数(a被移动后的长度)
*/
int shift(int *a, int aLen, int shiftLen)
{
//a == 0
if (a[aLen - 1] == 0 && aLen == 1)
{
return 1;
}
for (int i = aLen + shiftLen - 1; i >= 0; i--)
{
if (i >= shiftLen)
a[i] = a[i - shiftLen];
else
a[i] = 0;
}
return aLen + shiftLen;
}
/**
* karatsuba算法计算 a * b
* @param [in] num1 被乘数
* @param [in] num1Len 数组num1的长度
* @param [in] num2 乘数
* @param [in] num2Len 数组num2的长度
* @param [out] result 计算结果
*
* @return 计算结果的位数(result长度)
*/
int karatsubaMultiply(int *num1, int num1Len, int *num2, int num2Len, int *result)
{
//递归结束
if (num1Len == 1 && num2Len == 1)
{
result[0] = num1[0] * num2[0] % 10;
result[1] = num1[0] * num2[0] / 10;
return result[1] == 0 ? 1 : 2;
}
// 将乘数和被乘数分成两部分表示
int maxLen = num1Len > num2Len ? num1Len : num2Len;
int mid = (maxLen) / 2;
int a[MAX_LEN / 2] = {0};//MAX_LEN -- 处理的最大位数
int b[MAX_LEN / 2] = {0};
int c[MAX_LEN / 2] = {0};
int d[MAX_LEN / 2] = {0};
for (int i = 0; i < mid; i++)
{
b[i] = num1[i];
d[i] = num2[i];
}
for (int i = mid; i < maxLen; i++)
{
a[i-mid] = num1[i];
c[i-mid] = num2[i];
}
//计算a+b 和 c+d ; 使用大数相加 add
int aPlusb[MAX_LEN] = {0};
int aPlusbLen = add(a, maxLen - mid, b, mid, aPlusb);
int cPlusd[MAX_LEN] = {0};
int cPlusdLen = add(c, maxLen - mid, d, mid, cPlusd);
int z0[MAX_LEN] = {0};
int z1[MAX_LEN] = {0};
int z2[MAX_LEN] = {0};
int z0Len = 0;
int z1Len = 0;
int z2Len = 0;
//递归 计算a*c (a+b)*(c+d) bd
z0Len = karatsubaMultiply(a, maxLen - mid, c, maxLen - mid, z0);
z1Len = karatsubaMultiply(aPlusb, aPlusbLen, cPlusd, cPlusdLen, z1);
z2Len = karatsubaMultiply(b, mid, d, mid, z2);
/**
* 计算(z0*10^(2*m))+((z1-z2-z0)*10^(m))+(z2)
*
* z0 = a*c
* z1 = [(a+b)∗(c+d)−a*c−b*d]
* z2 = b*d
*/
// 1. z0*10^(2*m) --- r0
int z0Copy[MAX_LEN] = {0};
int z0CopyLen = z0Len;
for (int i = 0; i < MAX_LEN; i++)
z0Copy[i] = z0[i];
z0Len = shift(z0, z0Len, 2 * mid);
// 2. (z1-z2-z0)*10^(m)
//z1 - z2
int z1subz2Result[MAX_LEN] = {0};
int ne = 0;
int z1subz2Len = sub(z1, z1Len, z2, z2Len, z1subz2Result, &ne);
//(z1-z2) - z0
int z1subz2Andz0Result[MAX_LEN] = {0};
int z1subz2AndZ0Len = sub(z1subz2Result, z1subz2Len, z0Copy, z0CopyLen, z1subz2Andz0Result, &ne);
z1subz2AndZ0Len = shift(z1subz2Andz0Result, z1subz2AndZ0Len, mid);
int r1[MAX_LEN] = {0};
//3. (z0*10^(2*m))+((z1-z2-z0)*10^(m))+(z2)
int r1Len = add(z0, z0Len, z1subz2Andz0Result, z1subz2AndZ0Len, r1);
return add(r1, r1Len, z2, z2Len, result);
}
5, 除法
将除法转化成减法,比如 $9999 \div 99$ , 9999 不断减99,获得最终由多少个99构成,然而,如果是$9999 \div 1$, 这种方法就需要循环很多次,效率很低。我们可以先将1乘以1000,计算千位上的“商”–减的次数,之后计算百位上的次数,如此类推:
- 将除数通过向左移位,使其和被除数位数一样
- 被除数减除数,直至小于移位后的除数,记录减的次数(商)
- 除数左移一位,继续上述步骤,直至小于除数
以计算236 / 13为例:
| 步骤 | 操作 | 描述 |
|---|---|---|
| 1 | 13左移一位130 | 移位到和被除数位数相同 |
| 2 | 236减130; ans[1]++ |
记录减的次数 |
| 3 | 106 < 130; 130右移一位(13) | 被除数小于移位后的除数,除数左移一位 |
| 4 | 106 减 13; ans[0]++ |
注意:对应位记录减的次数 |
| 5 | 93 减 13 ; ans[0]++ |
对应位减的次数加一 |
| 6 | … | 循环操作,直到被除数小于13 |
代码如下:
/**
* 计算 a / b
* @param [in] a 被除数
* @param [in] aLen 数组a的长度
* @param [in] b 除数
* @param [in] bLen 数组b的长度
* @param [out] result 商(未计算余数)
*
* @return 计算结果的位数(result长度)
*/
int div(int *a, int aLen, int *b, int bLen, int *result)
{
int comResult = compareNum(a, aLen, b, bLen);
if (comResult == 0)
{
result[0] = 1;
return 1;
}
else if (comResult < 0)
{
result[0] = 0;
return 1;
}
int tempA[MAX_LEN] = {0};
int tempB[MAX_LEN] = {0};
int subResult[MAX_LEN] = {0};
int tempALen = aLen;
int tempBLen = bLen;
int subResultLen = 0;
for (int i = 0; i < aLen; i++)
{
tempA[i] = a[i];
}
for (int i = 0; i < bLen; i++)
{
tempB[i] = b[i];
}
int ne = 1;
int nowPos = aLen - bLen;//nowPos存储除数需要移动的位数
tempBLen = shift(tempB, tempBLen, nowPos); //tempB存放移位后的除数
while(1)
{
while(1)
{
ne = 1;
subResultLen = sub(tempA, tempALen, tempB, tempBLen, subResult, &ne);
//被除数小于移位后的除数,跳出本次减法循环,将除数右移一位[代码里重新左移除数]
if (ne < 0)
{
nowPos--;
break;
}
// tempA保存被减后的 被除数 的值,留待下一次计算
tempALen = subResultLen;
for (int i = 0; i < tempALen; i++)
tempA[i] = subResult[i];
//在对应位上记录减法的次数(“商”)
result[nowPos]++;
}
//所有位置计算完成,退出循环
if (nowPos < 0)
break;
//这里按照新的pos,左移除数(作用等同于右移一位)
//实际再写一个右移函数,更好一些
for (int i = 0; i < MAX_LEN; i++)
{
if (i < bLen)
tempB[i] = b[i];
else
tempB[i] = 0;
}
tempBLen = shift(tempB, bLen, nowPos);
}
//去除前面的0
if (result[aLen - bLen] != 0)
return aLen - bLen + 1;
else
return aLen - bLen;
}